In the given figure, EF = CE = CA, What is the value (in degrees) of $$\angle$$EAC?
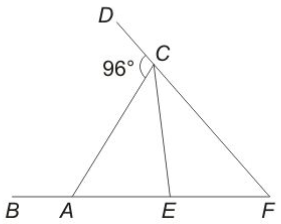
Solution

Given : EF = CE = CA
=> $$\angle$$ CAE = $$\angle$$ CEA = $$x$$ and $$\angle$$ ECF = $$\angle$$ EFC = $$y$$
To find : $$\angle$$ EAC = $$x=?$$
Solution : Using exterior angle property, => $$\angle$$ CAE + $$\angle$$ CFE = $$\angle$$ ACD
=> $$x+y=96^\circ$$ -----------------(i)
Also, $$\angle$$ CEF = $$(180^\circ-2y)=180^\circ-x$$
=> $$x=2y$$ ------------(ii)
Substituting it in equation (i), => $$2y+y=3y=96^\circ$$
=> $$y=\frac{96}{3}=32^\circ$$
$$\therefore$$ $$x=2\times32=64^\circ$$
=> Ans - (B)
Create a FREE account and get:
- Free SSC Study Material - 18000 Questions
- 230+ SSC previous papers with solutions PDF
- 100+ SSC Online Tests for Free

