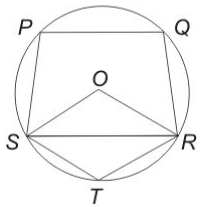
In the given figure, O is the center of the circle, $$\ \angle$$PQR = 100$$^\circ\ $$and $$\angle$$STR = 105$$^\circ$$. What is the value (in degrees) of $$\ \angle$$OSP?

Given : $$\ \angle$$PQR = 100$$^\circ\ $$and $$\angle$$STR = 105$$^\circ$$

To find : $$\ \angle$$OSP = ?

Solution : Quadrilateral PQRS is cyclic quadrilateral, hence opposite angles are supplementary.

=> $$\angle$$ PQR + $$\angle$$ PSR = $$180^\circ$$

=> $$\angle$$ PSR = $$180^\circ-100^\circ=80^\circ$$ --------------(i)

Also, angle at the centre is double the angle at any point on the circumference of the circle in the same segment.

=> reflex ($$\angle$$ SOR) = $$2$$ $$\times$$ $$\angle$$ STR

=> reflex ($$\angle$$ SOR) = $$2\times105^\circ=210^\circ$$

Thus, $$\angle$$ SOR = $$360^\circ-210^\circ=150^\circ$$

Now, in $$\triangle$$ SOR, OS = OR = radius

=> $$\angle$$ OSR = $$\angle$$ ORS = $$15^\circ$$ ----------(ii)

Subtracting equation (ii) from (i), we get :

$$\therefore$$ $$\angle$$ OSP = $$80^\circ-15^\circ=65^\circ$$

=> Ans - (D)