Question 134

The length of tangent drawn from an external point P to a circle of radius 5 cm is 12 cm. The distance of P from the centre of the circle is

Solution

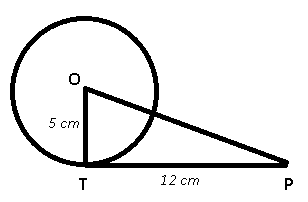
Given : OT is radius of circle = 5 cm and tangent PT = 12 cm

To find : OP = ?

Solution : The radius of a circle intersects the tangent at right angle, => $$\angle OTP = 90^\circ$$

Thus in $$\triangle$$ OPT,

=> $$(OP)^2=(PT)^2+(OT)^2$$

=> $$(OP)^2=(12)^2+(5)^2$$

=> $$(OP)^2=144+25=169$$

=> $$OP=\sqrt{169}=13$$ cm

=> Ans - (C)

Create a FREE account and get: