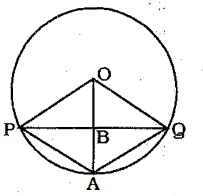
Chord PQ is the perpendicular bisector of radius OA of circle with center O (A is a point on the edge of the circle). If the length of Arc PAQ = $$\frac{2\pi}{3}$$. What is the length of chord PQ ?

.

PQ is perpendicular bisector of OA. Also, OP = OQ (radii)

Hence, OPAQ is a rhombus. --------------(i)

Also, $$2\angle PAQ=$$ reflex $$\angle POQ$$     [The angle subtended at the centre by an arc is twice to that at the circumference]

=> $$2\angle PAQ=360^\circ-\angle POQ$$

=> $$2\angle PAQ+\angle POQ=360^\circ$$

From (i), we have $$\angle PAQ=\angle POQ$$

=> $$3\angle POQ=360^\circ$$

=> $$\angle POQ=120^\circ=\frac{2\pi}{3}$$

We know that, $$r=\frac{l}{\theta}$$

=> $$r=\frac{\frac{2\pi}{3}}{\frac{2\pi}{3}}=1$$ unit

In $$\triangle$$ POB,

=> $$sin(\angle POB)=\frac{PB}{OP}$$

=> $$sin(60^\circ)=\frac{PB}{1}$$

=> $$PB=\frac{\sqrt3}{2}$$

$$\therefore$$ Chord PQ = $$2\times(PB)=2\times\frac{\sqrt3}{2}=\sqrt3$$

=> Ans - (B)