Question 115

ABC is an equilateral triangle. Points D, E, F are taken in sides AB, BC, CA respectively, so that AD = CF. Then AE, BF, CD enclosed a triangle which is:

Solution

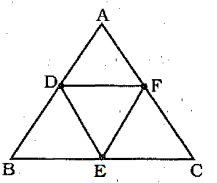
It is given that AB = BC = AC

=> (AD + BD) = (AF + CF)

$$\because$$ AD = CF, => BD = AF

Hence, AD = BD = BE = EC = CF = AF

$$\therefore$$ D, E and F are mid points of sides AB, BC and AC respectively.

Thus, DF $$\parallel$$ BC and DF = $$\frac{1}{2}$$ BC

Hence, DE = EF = DF

=> $$\triangle$$ DEF is equilateral triangle.

=> Ans - (A)

Create a FREE account and get: