Question 68

In quadrilateral $$ABCD, \angle C = 72^\circ$$ and $$\angle D = 28^\circ$$. The bisectors of $$\angle A$$ and $$\angle B$$ meet in O. What is the measure of $$\angle AOB$$?

Solution

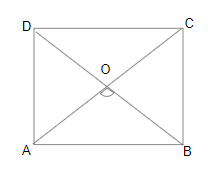
In quadrilateral $$ABCD$$,
$$\angle A + \angle B + \angle C + \angle D$$ = 360
$$\angle A + \angle B = 360 - 72 - 28 = 260\degree$$
$$\frac{1}{2}(\angle A + \angle B) = 130\degree$$
In $$\triangle$$ AOB,
$$\frac{1}{2}(\angle A + \angle B) + \angle AOB = 180$$
$$\angle AOB = 180 - 130 = 50\degree$$

Create a FREE account and get:

Free SSC Study Material - 18000 Questions
230+ SSC previous papers with solutions PDF
100+ SSC Online Tests for Free

CAT Quant Questions | CAT Quantitative Ability

CAT Algebra Questions CAT Data Sufficiency Questions CAT Time, Distance and Work Questions CAT Number Systems Questions CAT Linear Equations Questions

CAT DILR Questions | LRDI Questions For CAT

CAT DI with connected data sets Questions CAT Routes And Networks Questions CAT Special Charts Questions CAT Table with Missing values Questions CAT Selection With Condition Questions

CAT Verbal Ability Questions | VARC Questions For CAT

CAT Vocabulary Questions CAT Miscellaneous Questions CAT Odd One Out Questions CAT Verbal Ability Questions CAT Critical Reasoning Questions

SSC CGL Tier-2 13th September 2019 Maths

In quadrilateral $$ABCD, \angle C = 72^\circ$$ and $$\angle D = 28^\circ$$. The bisectors of $$\angle A$$ and $$\angle B$$ meet in O. What is the measure of $$\angle AOB$$?

CAT Quant Questions | CAT Quantitative Ability

CAT DILR Questions | LRDI Questions For CAT

CAT Verbal Ability Questions | VARC Questions For CAT

Free Quant Questions

Login to your Cracku account

Hello! 👋

Ready to Unlock Your Success?

Please Enter Your OTP

Please enter the following details

Create a free Cracku account