In $$\triangle$$ABC, $$\angle$$A = 90°. If BL and CM are the medians, then:

Solution

It is given the question that,
$$\triangle$$ABC, $$\angle$$A = 90°
BL and CM are the medians, so $$AL=LC=\dfrac{AC}{2} and AM=MB=\dfrac{AB}{2}$$

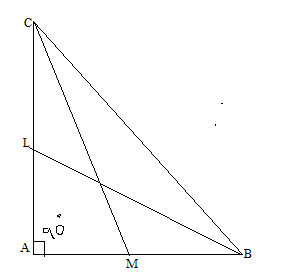
Now, in the right angled triangle $$\triangle CAM$$, applying the Pythagoras theorem
$$AC^2+AM^2=CM^2$$---------(i)
In the right angled triangle $$\triangle LAB$$, applying the Pythagoras theorem
$$AL^2+AB^2=LB^2$$----------(ii)
in the right angled triangle $$\triangle CAB$$, applying the Pythagoras theorem
$$AC^2+AB^2=BC^2$$----------(iii)
From the equation (i) and (ii)
$$AC^2+AM^2+AL^2+AB^2=CM^2+LB^2$$
$$AC^2+(\dfrac{AB}{2})^2+(\dfrac{AC}{2})^2+AB^2=CM^2+LB^2$$
$$AC^2+\dfrac{AB^2}{4}+\dfrac{AC^2}{4}+AB^2=CM^2+LB^2$$
$$\dfrac{5AB^2}{4}+\dfrac{5AC^2}{4}=CM^2+LB^2$$
$$5(\dfrac{AB^2}{4}+\dfrac{AC^2}{4})=CM^2+LB^2$$
$$5(AB^2+AC^2)=4(CM^2+LB^2)$$-------(iv)
From the equation (iii) and (iv)
$$4(CM^2+LB^2)=5BC^2$$
$$4(BL^2+CM^2)=5BC^2$$