ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and $$\angle$$ADC = 126$$^\circ$$. $$\angle$$BAC is equal to:

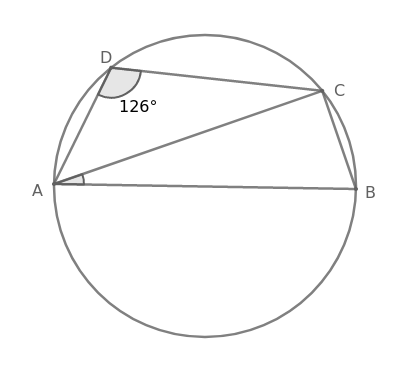
In cyclic quadrilateral ABCD, sum of opposite angles = 180$$^\circ$$

$$=$$>  $$\angle$$ADC + $$\angle$$ABC = 180$$^\circ$$

$$=$$>   126$$^\circ$$ + $$\angle$$ABC = 180$$^\circ$$

$$=$$>   $$\angle$$ABC = 54$$^\circ$$

Angle subtended by diameter in a semicircle is 90$$^\circ$$

$$=$$>  $$\angle$$ACB = 90$$^\circ$$

In $$\triangle\ $$ACB,

$$\angle$$BAC + $$\angle$$ACB + $$\angle$$ABC = 180$$^\circ$$

$$=$$>  $$\angle$$BAC + 90$$^\circ$$ + 54$$^\circ$$ = 180$$^\circ$$

$$=$$>  $$\angle$$BAC + 144$$^\circ$$ = 180$$^\circ$$

$$=$$>  $$\angle$$BAC = 36$$^\circ$$

Hence, the correct answer is Option D