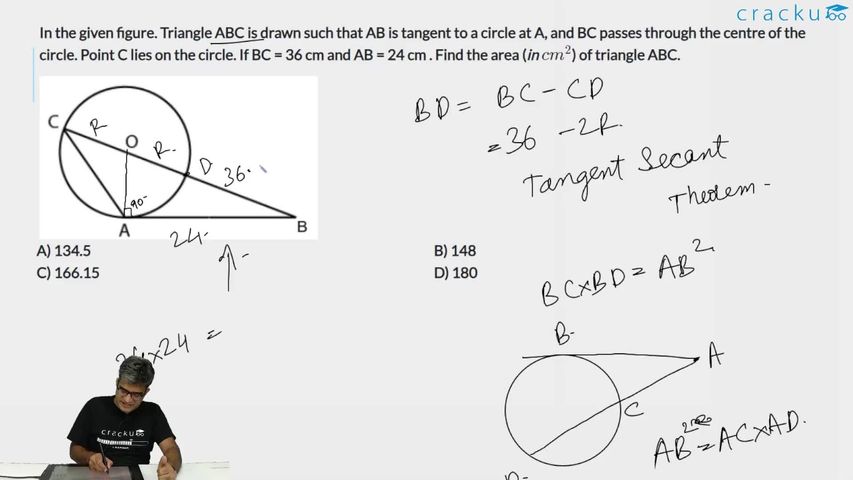
In the given figure. Triangle ABC is drawn such that AB is tangent to a circle at A, and BC passes through the centre of the circle. Point C lies on the circle. If BC = 36 cm and AB = 24 cm . Find the area (in $$cm^2$$) of triangle ABC. 

OAB will be a right-angled triangle where OA is a radius and it is perpendicular to AB.
We know AB =  24 cm and BC = 26 cm . 
Let the radius of circle be "r" . 

In right angle triangle OAB :  $$OB=r+36-2r=36-r$$

$$OA^2+AB^2=OB^2$$
$$r^2+24^2=(36-r)^2$$
$$24^2=36^2-72r$$
$$r=10cm$$. 

Triangle OAC is isosceles triangle.
 If $$\angle\ OAC=\theta\ $$ $$\rightarrow$$ $$\angle\ AOB=2\theta\ $$  and $$\angle\ ABO=90-2\theta\ $$ . 

Hence, from right angled triangle : $$\cos\left(90-2\theta\right)=\sin2\theta\ =\dfrac{\ 24}{36-r}=\dfrac{\ 24}{26}=\dfrac{\ 12}{13}$$

Hence, area of triangle ABC = area(OAB) + area(OCA)
                                          $$=\ \dfrac{\ 1}{2}\left(r\right)\left(24\right)+\ \dfrac{\ 1}{2}\left(r\right)\left(r\right)\sin\left(180-2\theta\ \right)$$ 

                                         $$=12\left(10\right)+50\ \left(\dfrac{\ 12}{13}\right)$$

                                            = $$120+46.15$$

                                            $$=166.15\ sq.cm$$.