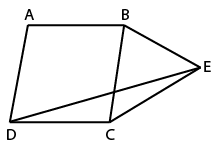
In the given figure, ABCD is a rhombus and BCE is an isosceles triangle, with BC = CE, ∠CBE = 84° and ∠ADC = 78°, then what is the value (in degrees) of ∠DEC? 

Given : BC = CE, ∠CBE = 84° and ∠ADC = 78°

To find : ∠DEC = $$\theta$$ = ?

Solution : Adjacent angles of a rhombus are supplementary

=> ∠ADC + ∠BCD = $$180^\circ$$

=> ∠BCD = $$180-78=102^\circ$$ ---------------(i)

$$\triangle$$ BCE is an isosceles triangle with BC = CE, => ∠CBE = ∠CEB = 84°

Thus, in $$\triangle$$ BCE,

=> ∠CBE + ∠CEB + ∠BCE = $$180^\circ$$

=> ∠BCE = $$180-84-84=12^\circ$$ ---------------(ii)

Adding equations (i) and (ii),

=> ∠BCD + ∠BCE = $$102+12$$

=> ∠DCE = $$114^\circ$$

Now, ABCD is a rhombus and BC = CE, => CD = CE and thus CDE is an isosceles triangle with ∠CDE = ∠DEC = $$\theta$$

In $$\triangle$$CDE

=> $$\theta+\theta+\angle DCE = 180^\circ$$

=> $$2\theta = 180-114=66^\circ$$

=> $$\theta = \frac{66}{2}=33^\circ$$

=> Ans - (C)