In the given figure, $$\triangle$$PQR is drawn such that PQ is tangent to a circle whose radius is 10 cm and QR passes through centre of the circle. Point R lies on the circle. If QR = 36 cm, then what is the area (in cm$$^{2}\ $$of $$\ \triangle$$PQR?

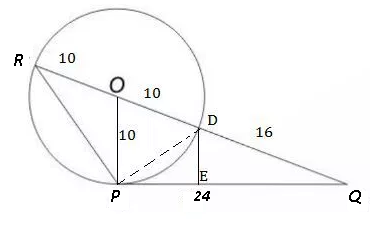
Given : OP = OR = 10 cm and QR = 36 cm

=> DQ = 16 cm and $$PQ=\sqrt{(26)^2-(10)^2}=24$$ cm

Area of $$\triangle$$ POQ = $$\frac{1}{2}\times(PQ)\times(OP)$$

= $$\frac{1}{2}\times24\times10=120$$ $$cm^2$$ -----------(i)

Now, draw DE $$\parallel$$ OP, such that $$\triangle$$ DEQ $$\sim$$ $$\triangle$$ OPQ

=> $$\frac{DQ}{OQ}=\frac{DE}{OP}$$

=> $$DE=\frac{16}{26}\times10=\frac{80}{13}$$ cm

Thus, area of $$\triangle$$ PDQ = $$\frac{1}{2}\times\frac{80}{13}\times24\approx74$$ $$cm^2$$ ---------------(ii)

Also, in $$\triangle$$ PRD, OP is the median, thus $$ar(\triangle OPR)=ar(\triangle DOP)$$

= $$ar(\triangle POQ)-ar(\triangle PDQ)$$

Subtracting equation (ii) from (i), we get :

=> Area of $$\triangle$$ DOP = $$120-74=46$$ $$cm^2$$ --------------(iii)

$$\therefore$$ Area of $$\triangle$$ PQR = $$120+46\approx166$$ $$cm^2$$      [Adding equation (i) and (iii)]

=> Ans - (C)