On a circular path of radius 6 m a boy starts from a point A on the circumference and walks along a chord AB of length 3 m. He then walks along another chord BC of length 2 m to reach point C. The point B lies on the minor arc AC. The distance between point C from point A is
Solution
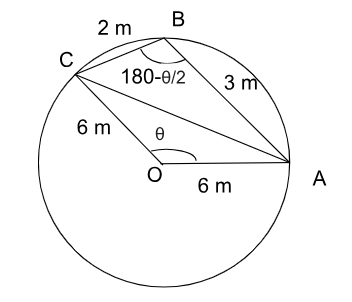
Let the distance AC be $$x$$ metres
Also, let the chord AC subtend an angle $$\theta\ $$ at the centre of the circle.
So, angle subtended by the chord AC on minor arc i.e. at point B will be $$180-\dfrac{\theta}{2}\ $$
Now, applying cosine rule in $$\triangle\ OAC$$,
$$\cos\theta\ =\dfrac{6^2+6^2-x^2}{2\times\ 6\times\ 6}=\dfrac{72-x^2}{72}$$ ------>(1)
Also, applying cosine rule in $$\triangle\ BAC$$,
$$\cos\left(180-\dfrac{\theta}{2}\right)\ =\dfrac{2^2+3^2-x^2}{2\times\ 2\times\ 3}$$
or, $$-\cos\dfrac{\theta}{2}\ \ =\dfrac{2^2+3^2-x^2}{2\times\ 2\times\ 3}=\dfrac{13-x^2}{12}$$ -------->(2)
Now we know,
$$\cos\theta\ =2\cos^2\dfrac{\theta}{2}-1$$
So from (1) and (2) we can say,
$$\dfrac{\left(72-x^2\right)}{72}=2\left(\dfrac{13-x^2}{12}\right)^2-1$$
or, $$\dfrac{\left(72-x^2\right)}{72}=\dfrac{\left(13-x^2\right)^2}{72}-1$$
or, $$72-x^2=\left(13-x^2\right)^2-72$$
or, $$72-x^2=169-26x^2+x^4-72$$
or, $$x^4-25x^2+25=0$$
or, $$x^2=\dfrac{25+\sqrt{\ \left(25^2-4\times\ 25\times\ 1\right)}}{2}=\dfrac{25+\sqrt{\ 525}}{2}$$ (we can't take negative root as $$x^2$$ is always positive)
or,$$x^2=\dfrac{50+2\sqrt{\ 525}}{4}=\dfrac{\left(\sqrt{\ 15}\right)^2+\left(\sqrt{\ 35}\right)^2+2\sqrt{\ 15}\times\ \sqrt{\ 35}}{4}=\left(\dfrac{\sqrt{\ 15}+\sqrt{\ 35}}{2}\right)^2$$
or, $$x=\dfrac{\sqrt{\ 15}\ +\ \sqrt{\ 35}}{2}$$ m
Create a FREE account and get:
- Download Maths Shortcuts PDF
- Get 300+ previous papers with solutions PDF
- 500+ Online Tests for Free

