Question 32

Points P, Q, R and S are taken on sides AB, BC, CD and DA of square ABCD respectively, so that AP : PB = BQ : QC = CR : RD = DS : SA = 1 : n . Then the ratio of the area of PQRS to the area of ABCD is

Solution

Let the side of square be $$(n+1)$$ units.

So we can make a diagram like:

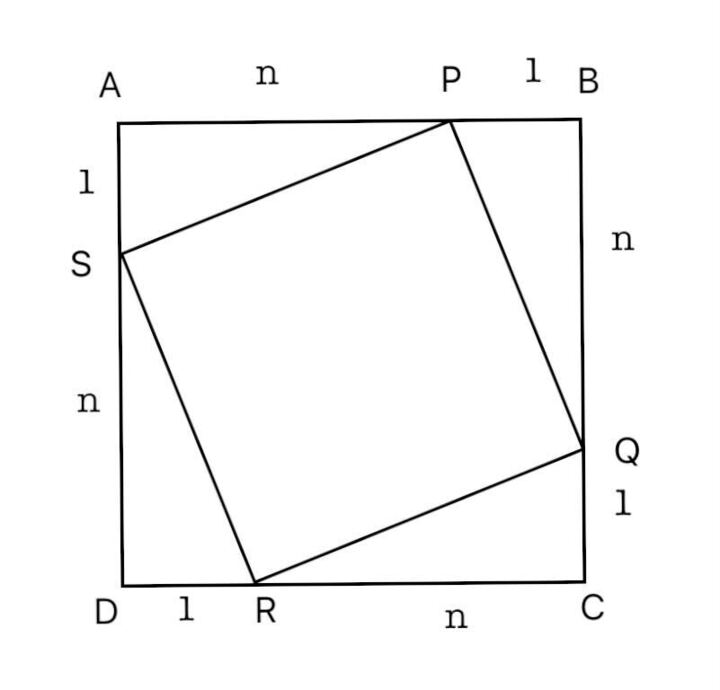
Now $$\triangle\ QRC$$ is a right angled triangle.

So, $$RQ=\sqrt{\ QC^2+RC^2}=\sqrt{\ n^2+1}$$

So, area of square $$PQRS$$=$$\left(\sqrt{\ n^2+1}\right)^2$$ = $$n^2+1$$

Area of ABCD = $$\left(n+1\right)^2$$

So, required ratio = $$\dfrac{n^2+1}{\left(n+1\right)^2}$$

View More Questions From Temporary

Create a FREE account and get: