A chord is drawn inside a circle, such that the length of the chord is equal to the radius of the circle. Now, two circles are drawn, one on each side of the chord, each touching the chord at its midpoint and the original circle. Let k be the ratio of the areas of the bigger inscribed circle and the smaller inscribed circle, then k equals

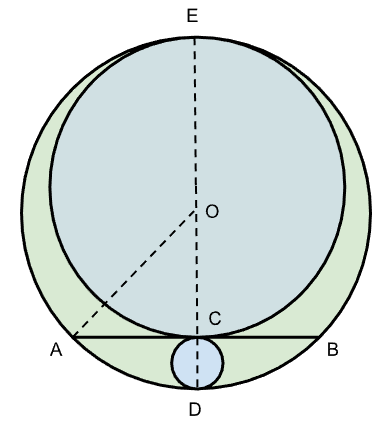
Since the other two circles drawn on the chord are touching the midpoint of the chord, the centre of all three circles lies on the same line. 

Let O be the centre of the main circle (Green Coloured), and the radius of that be 2R. Thus, AO = 2R.

Now, AB is the chord such that the length of the chord is equal to the radius of the circle. Thus, AB = 2R => AC = R

Now, $$OC^2+AC^2=OA^2$$ => $$OC^2+R^2=4R^2$$ => $$OC=\sqrt{3}R$$

Let the radius of the smaller circle below the chord be 'a', and the radius of the bigger circle above the chord be 'A'. 

Then, CD = 2a and OD = 2R

=> $$OC+CD=OD$$

=> $$\sqrt{3}R+2a=2R$$

=> $$a=\dfrac{\left(2-\sqrt{3}\right)R}{2}$$

Also, $$OC+OE=2A$$, and OE = 2R

=> $$\sqrt{3}R+2R=2A$$

=> $$A=\dfrac{\left(\sqrt{3}+2\right)R}{2}$$

=> Ratio of area of larger circle to area of smaller circle = $$\dfrac{\pi A^2}{\pi a^2}$$

=> Ratio of area of larger circle to area of smaller circle = $$\dfrac{\left[\frac{R\left(2+\sqrt{3}\right)}{2}\right]^{^2}}{\left[\frac{R\left(2-\sqrt{3}\right)}{2}\right]^{^2}}$$

=> Ratio of area of larger circle to area of smaller circle = $$\dfrac{7+4\sqrt{3}}{7-4\sqrt{3}}$$

Rationalising the numerator and the denominator - 

=> Ratio of area of larger circle to area of smaller circle = $$\dfrac{7+4\sqrt{3}}{7-4\sqrt{3}}\times\dfrac{7+4\sqrt{3}}{7+4\sqrt{3}}$$

=> Ratio of area of larger circle to area of smaller circle = $$\dfrac{49+48+56\sqrt{3}}{49-48}$$

=> Ratio of area of larger circle to area of smaller circle = $$97+56\sqrt{3}:1$$