Please enter the following details
Free Daily Targets & Mocks
Study Material & Formulas PDFs
1 on 1 Mentorship
Question 26
.png)
In the given figure, $$B$$ and $$C$$ are the centres of the two circles. $$ADE$$ is the common tangent to the two circles. If the ratio of the radius of both the circles is $$3 : 5$$ and $$AC = 40$$, then what is the value of $$DE$$
Solution
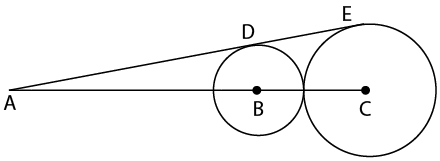
Now we have triangles ABD and ACE as similar triangles
Angle A is common and ADB=AEC=90
so we can say
AB:AC = BD:CE
we get AB = 3/5*40 =24
and BC =40-24=16
Now sum of radius =16
so r1 =6 and r2=10
Now DE is direct tangent and its length will be :$$\sqrt{\ 16^2-\left(10-6\right)^2}\ \ =\sqrt{\ 240\ }=4\sqrt{\ 15}$$
Create a FREE account and get:
- Free SSC Study Material - 18000 Questions
- 230+ SSC previous papers with solutions PDF
- 100+ SSC Online Tests for Free
