Question 143

ABCD is a square. Draw an equilateral triangle PBC on side BC considering BC is a base and an equilateral triangle QAC on digonal AC considering AC is a base. Find the value of $$\ \frac{Area \ of \ \triangle PBC}{Area \ of \ \triangle QAC}$$

Solution

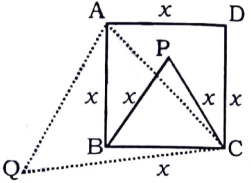
Let side of the square be $$x$$ cm

=> Side of equilateral $$\triangle$$ PBC = $$x$$ cm

In right $$\triangle$$ ABC,

=> $$(AC)^2=(AB)^2+(BC)^2$$

=> $$(AC)^2=(x)^2+(x)^2=2x^2$$

=> $$AC=\sqrt2x$$

$$\therefore$$ $$\ \frac{ar(\triangle PBC)}{ar(\triangle QAC)}$$

= $$[\frac{\sqrt3}{4}\times (x)^2]\div[\frac{\sqrt3}{4}\times (\sqrt2x)^2]$$

= $$\frac{x^2}{2x^2}=\frac{1}{2}$$

=> Ans - (A)

Create a FREE account and get: