Question 137

A chord of length 7 cm subtends an angle of 60° at the centre of a circle. What is the radius (in cm) of the circle?

Solution

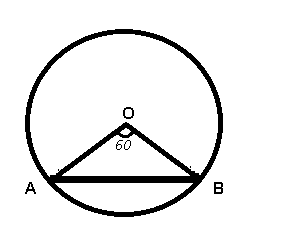
Given : AB = 7 cm and $$\angle O=60^\circ$$

To find : OA = OB = $$r=?$$

Solution : In $$triangle$$ OAB, we have $$OA=OB=r$$

=> $$\angle A=\angle B$$

=> $$\angle A+\angle B+\angle O=180^\circ$$

=> $$2\angle A=180^\circ-60^\circ=120^\circ$$

=> $$\angle A=\frac{120^\circ}{2}=60^\circ$$

$$\therefore$$ $$\triangle$$ OAB is equilateral triangle and OA = OB = $$r=7$$ cm

=> Ans - (C)

Create a FREE account and get: