A circle passing through points Q and R of triangle PQR, cuts the sides PQ and PR at points X and Y respectively. If PQ = PR, then what is the value (in degrees) of $$\angle$$PRQ + $$\angle$$QXY ?

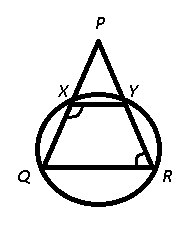
Given : PQR is an isosceles triangle, PQ = PR

To find : $$\angle$$PRQ + $$\angle$$QXY = ?

Solution : Since, $$\triangle$$ PQR is isosceles, we have $$\angle Q=\angle R$$

Now, XY is parallel to QR, and sum of angles on the same side of transversal is supplementary, => $$\angle PQR+\angle QXY=180^\circ$$

=> $$\angle$$PRQ + $$\angle$$QXY = $$180^\circ$$

II method : XYRQ is a cyclic quadrilateral and opposite angles in a cyclic quadrilateral are supplementary.

=> Ans - (D)