Two identical circles each of radius 2 cm interest each other such that the circumference of each one passes through the centre of the other. What is the area (in cm$$^{2})\ $$of the intersecting region ?

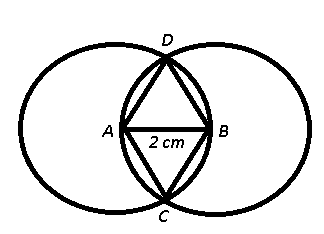
In above diagram, AB = AC = BC = 2 cm, thus $$triangle$$ ABC and $$triangle$$ ABD are equilateral triangles.

=> $$\angle$$ DAC = $$\angle$$ BAC + $$\angle$$ DAB = $$60^\circ+60^\circ=120^\circ$$

Also, area of both sectors CBD and CAD are equal.

Now, area of enclosed region = $$2$$ $$\times$$ ar(sector CAD) - $$2$$ $$\times$$ ar($$\triangle$$ CAB)$$

= $$(2\times\frac{120^\circ}{360^\circ}\pi r^2)-(2\times\frac{\sqrt3}{4}r^2)$$

= $$(\frac{2}{3}\pi\times4)-(\frac{\sqrt3}{2}\times4)$$

= $$\frac{8\pi}{3}-2\sqrt{3}$$

=> Ans - (A)