SSC CGL 23rd August 2021 Shift-3
For the following questions answer them individually
$$\triangle ABC$$ is an equilateral triangle with side 18 cm. D is a point on BC such that $$BD = \frac{1}{3}BC$$ Then length(in cm) of AD is:
The given histogram represents the marks obtained by 128 students. Read the graph and answer the question that follows.
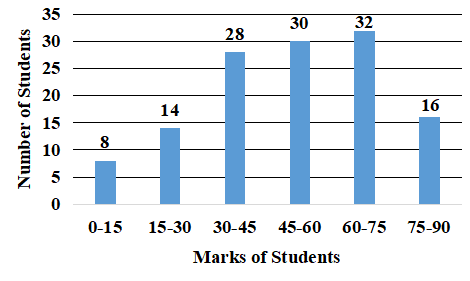
What percent of students got marks less than 60?
If the 9-digit number 89x64287y is divisible by 72, then what is the value of (3x + 2y)?
There are some children in a camp andtheir average weightis 40 kg. If 5 children with average weight 36 kg join the camp orif 5 children with average weight 43.2 kg leave the camp, the average weightof children in both cases is equal. How manychildren are there in the camp, initially?
Lucky spends 85% of her income. If her expenditure increases by x %, savings increase by 60% and income increases by 26%, then what is the value of x ?
A person borrowed a sum of ₹30800 at 10% p.a. for 3 years, interest compounded annually. At the end of two years, he paid a sum of ₹13268. At the end of 3rd year, he paid ₹ x to clear of the debt. What is the value of x ?
If $$9(a^2 + b^2) + c^2 + 20 = 12(a + 2b)$$, then the value of $$\sqrt{6a + 9b + 2c}$$ is:
The marked price of an article is ₹180. Renu sells it after 20% discount on its marked price and still gains 25%, The cost price (in ₹) of the article is:
If $$\frac{1}{1 - \sin \theta} + \frac{1}{1 + \sin \theta} = 4 \sec \theta, 0^\circ < \theta < 90^\circ$$, then the value of $$\cot\theta+\operatorname{cosec}\theta$$ is:
The bisector of $$\angle A$$ in $$\triangle ABC$$ meets side BC at D. If AB = 12 cm, AC = 15 cm and BC = 18 cm, then the length of DC is:
