SSC CGL 20th August 2021 Shift-1
For the following questions answer them individually
In circle with centre O and radius 13 cm, a chord AB is drawn. Tangentsat A and B intersect at P such that $$\angle APB = 60^\circ$$. If Distance of AB from the centre O is 5 cm, then what is the length (in cm) of AP?
The table shows the daily income of 50 persons.
Study the table and answer the question.
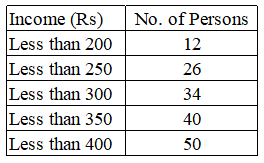
What is the ratio of the number of persons earning less than ₹200 to the number of persons earning ₹300 or more?
In a circle, chords AB and CD intersect internally, at E. If CD = 16 cm, DE = 6 cm, AE = 12 cm, and BE = X cm then the value of x is:
The ratio of two numbers A and B is 5 : 8. If 5 is added to each of A and B, then the ratio becomes 2 : 3. The difference in A and B is:
If $$\sec(5 \alpha - 15^\circ) = \cosec(15^\circ - 2 \alpha)$$, then the value of $$\cos \alpha + \sin 2 \alpha + \tan(1.5 \alpha)$$ is:
If $$\sin(20 + x)^\circ = \cos 60^\circ, 0 \leq (20 + x) \leq 90$$, then find the value of $$2 \sin^2(3x + 15)^\circ - \cosec^2(2x + 10)^\circ$$.
Weight of A is 20% more than weight of B, whose weight is 30% more than weight of C. By how much percent weight of A is more than weight of C?
A takes 2 hours more than B to cover a distance of 40 km. If A doubles his speed, he takes $$1\frac{1}{2}$$ hour more than B to cover 80 km. To cover a distance of 120 km, how much time(in hours) will B take travelling at his same speed?
If $$\left(2a+\frac{3}{a}-1\right)=11$$, what is the value of $$\left(4a^2 + \frac{9}{a^2}\right)?$$
