In the given figure, PM is one-third of PQ and PN is one-third of PS. If the area of PMRN is 17 cm2, then what is the area $$(in cm^2)$$ of PQRS?
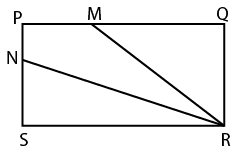
Solution
Let PQ = SR = $$3l$$ and PS = QR = $$3b$$ cm
=> QM = $$2l$$ and NS = $$2b$$
Let the area of rectangle PQRS = $$9lb=x$$ $$cm^2$$ --------------(i)
=> Area of rectangle PQRS = Area of PMNR + ar($$\triangle$$ NSR) + ar($$\triangle$$ QMR)
=> $$x=17+(\frac{1}{2}\times NS\times SR)+(\frac{1}{2}\times QM\times QR)$$
=> $$x=17+(\frac{1}{2}\times2b\times3l)+(\frac{1}{2}\times2l\times3b)$$
=> $$x=17+6lb$$
Multiplying equation (i) by $$\frac{2}{3}$$, => $$6lb=\frac{2x}{3}$$
=> $$x-\frac{2x}{3}=17$$
=> $$x=17\times3=51$$ $$cm^2$$
=> Ans - (B)
Create a FREE account and get:
- Free SSC Study Material - 18000 Questions
- 230+ SSC previous papers with solutions PDF
- 100+ SSC Online Tests for Free

