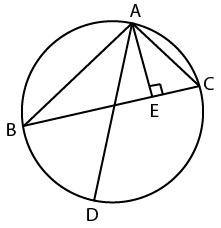
In the given figure. ABC is a triangle in which. AB = 10 cm. AC = 6 cm and altitude AE = 4 cm. If AD is the diameter of the circum-circle. then what is the length (in cm) of circum-radius? 

Given : AB = 10 cm. AC = 6 cm and altitude AE = 4 cm

To find : Circumradius = $$R$$ = ?

Solution : In $$\triangle$$ ACE,

=> $$(CE)^2=(AC)^2-(AE)^2$$

=> $$(CE)^2=(6)^2-(4)^2$$

=> $$(CE)^2=36-16=20$$

=> $$CE=\sqrt{20}$$ cm

Similarly, $$BE = \sqrt{100-16}=\sqrt{84}$$ cm

Now, BC = BE+CE = $$(\sqrt{20}+\sqrt{84})$$ cm

Area of $$\triangle$$ ABC = $$\frac{1}{2}\times(AE)\times(BC)$$

=> $$\triangle=\frac{1}{2}\times4\times(\sqrt{20}+\sqrt{84})$$

=> $$\triangle=2(\sqrt{20}+\sqrt{84})$$ $$cm^2$$

$$\therefore$$ Circumradius, $$R=\frac{abc}{4\triangle}$$

= $$\frac{10\times6\times(\sqrt{20}+\sqrt{84})}{4\times2(\sqrt{20}+\sqrt{84})}$$

= $$\frac{60}{8}=7.5$$ cm

=> Ans - (B)