Question 93

D and E are points on side AB and AC of ΔABC. DE is parallel to BC. If AD:DB = 2:5 and area of ΔADE is 8 sq cm, what is the ratio of area of ΔADE: area of quadrilateral BDEC?

Solution

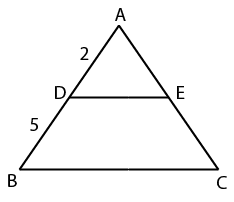
ADE & ABC are similar, let area of $$\triangle$$ ABC = x, that of DBCE = x-8

For similar triangles

Ratio of sides = $$\sqrt{ \text(ratio of areas)}$$

AB/AD = $$\sqrt{ \frac{area.ABC}{area.ADE}}$$

7/2 = $$\sqrt{ \frac{x}{8}}$$

49/4 = $$\frac{x}{8}$$

x = 98

area of quadrilateral BDEC = ABC - ADE = x - 8 = 98 - 8 = 90

$$\frac{ADE}{BDEC} = \frac{8}{90} = \frac{4}{45}$$

So the answer is option A.

Create a FREE account and get:

CAT Quant Questions | CAT Quantitative Ability