If $$ \triangle$$ABC, $$\angle$$ABC=90$$^\circ$$ and BD$$\bot$$AC , if AD = 4cm and CD = 5cm then BD is equal to

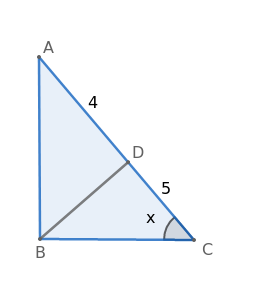
Let $$\angle\ $$C = x

In $$ \triangle$$ABC,

$$\cos x$$ = $$\frac{BC}{9}$$

$$=$$>  BC = 9 $$\cos x$$

In $$ \triangle$$BCD,

$$\cos x$$ = $$\frac{5}{BC}$$

$$=$$>  $$\cos x=\frac{5}{9\cos x}$$

$$=$$>  $$\cos^2x=\frac{5}{9}$$

$$=$$>  $$\cos x=\frac{\sqrt{5}}{3}$$

$$=$$>  $$\sin x=\sqrt{1-\cos^2x}=\sqrt{1-\frac{5}{9}}=\sqrt{\frac{4}{9}}=\frac{2}{3}$$

In $$ \triangle$$BCD,

$$\sin x=\frac{BD}{BC}$$

$$=$$>  $$\frac{2}{3}=\frac{BD}{9\cos x}$$

$$=$$>  $$\frac{2}{3}=\frac{BD}{9\left(\frac{\sqrt{5}}{3}\right)}$$

$$=$$>  $$\frac{2}{3}=\frac{3BD}{9\left(\sqrt{5}\right)}$$

$$=$$>  BD = 2$$\sqrt{5}$$

Hence, the correct answer is Option B