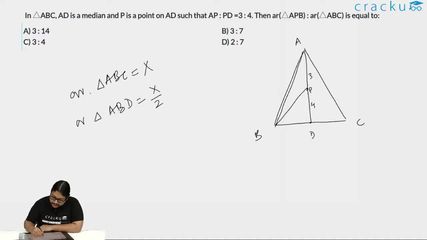
In $$\triangle$$ABC, AD is a median and P is a point on AD such that AP : PD =3 : 4. Then ar($$\triangle$$APB) : ar($$\triangle$$ABC) is equal to:

Given that,

In $$\triangle ABC$$, AD is the median.

And P is a point on AD such that AP : PD =3 : 4

We know that If two triangle have the same height and the length of the base is different then ratio of their area will be equal to the ratio of the respective base.

In $$\triangle$$ABC,

$$ar(\triangle ABD )=ar(\triangle ADC )=\dfrac{ar( \triangle ABC)}{2}$$

So, As per the area division rule of a triangle,

$$\Rightarrow \dfrac{ar(\triangle APB)}{ar(\triangle BPD)}=\dfrac{3}{4}$$

So, $$\Rightarrow ar(\triangle APB)=\dfrac{3 \times ar(\triangle ABD)}{3+4}$$

$$\Rightarrow ar(\triangle ABD)=\dfrac{3 \times ar(\triangle ABD)}{7}$$

Hence,
$$\Rightarrow ar(\triangle APB)$$ : $$ar(\triangle ABC)$$=$$\dfrac{\dfrac{3 \times ar(\triangle ABD)}{7}}{2 \times ar(\triangle ABD )}$$

$$\Rightarrow ar(\triangle APB)$$ : $$ar(\triangle ABC)$$=$$\dfrac{3}{14}$$