If one side of a triangle is 7 with its perimeter equal to 18, and area equal to $$\sqrt{108}$$, then the other two sides are:
Solution
Given,
One side of the triangle (a) = 7
Let the other two sides of the triangle are b and c
Perimeter of the triangle = 18
$$=$$> a+b+c = 18
$$=$$> 7+b+c = 18
$$=$$> b+c = 11 .................(1)
Semi perimeter of the triangle (s) = $$\frac{18}{2}=9$$
Area of the triangle = $$\sqrt{108}$$
$$=$$> $$\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}=\sqrt{108}$$
$$=$$> $$\sqrt{9\left(9-7\right)\left(9-b\right)\left(9-c\right)}=\sqrt{108}$$
$$=$$> $$9\left(2\right)\left(9-b\right)\left(9-c\right)=108$$
$$=$$> $$\left(9-b\right)\left(9-c\right)=6$$
$$=$$> $$81-9c-9b+bc=6$$
$$=$$> $$81-9\left(b+c\right)+bc=6$$
$$=$$> $$81-9\left(11\right)+bc=6$$
$$=$$> $$81-99+bc=6$$
$$=$$> $$bc=6+99-81$$
$$=$$> $$bc=24$$
$$=$$> $$c=\frac{24}{b}$$
Substituting $$c=\frac{24}{b}$$ in equation (1)
$$b+\frac{24}{b}=11$$
$$=$$> $$b^2+24=11b$$
$$=$$> $$b^2-11b+24=0$$
$$=$$> $$b^2-8b-3b+24=0$$
$$=$$> $$b\left(b-8\right)-3\left(b-8\right)=0$$
$$=$$> $$\left(b-8\right)\left(b-3\right)=0$$
$$=$$> $$b=8$$ or $$b=3$$
when $$b=8$$, $$c=\frac{24}{8}=3$$
when $$b=3$$, $$c=\frac{24}{3}=8$$
$$\therefore\ $$The other two sides of the triangle are 3 and 8
Hence, the correct answer is Option D
Video Solution
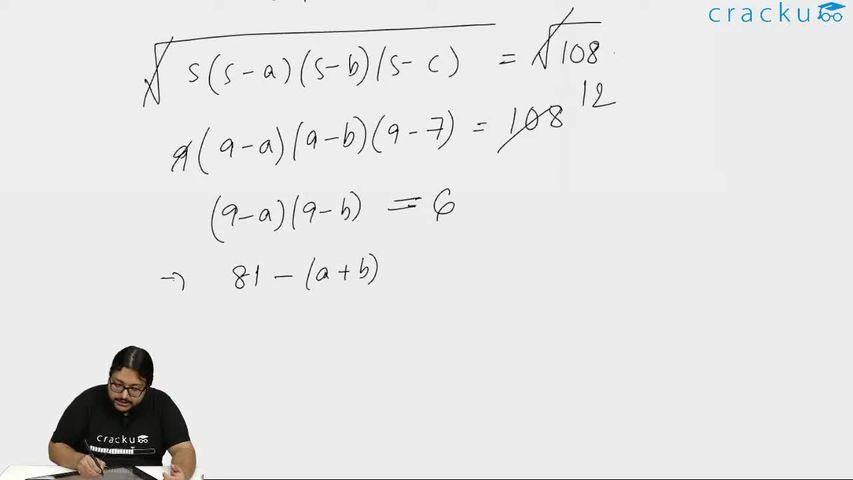
Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
- Free SSC Study Material - 18000 Questions
- 230+ SSC previous papers with solutions PDF
- 100+ SSC Online Tests for Free

