A circle is inscribed in an equilateral triangle and a square is inscribed in that circle. The ratio of the areas of the triangle and square is

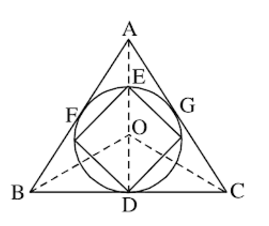
ABC is an equilateral triangle with side $$AB=a$$. AO, BO and CO are the angle bisectors of $$\angle$$ A, $$\angle$$ B and $$\angle$$ C respectively. O is the centre of the circle and let radius of circle = $$r$$ and side of square = $$s$$

Also, we know that the angle bisector from the vertex of an equilateral triangle is the perpendicular bisector of the opposite side.

=> AD is the perpendicular bisector of BC.

=> $$BD=\frac{a}{2}$$ and $$\angle$$ OBD = $$\frac{1}{2}\angle B=\frac{1}{2}\times60^\circ=30^\circ$$

Now, in $$\triangle$$ OBD,

=> $$tan(30^\circ)=\frac{OD}{BD}=\frac{r}{\frac{a}{2}}$$

=> $$r=\frac{1}{\sqrt3}\times\frac{a}{2}=\frac{a}{2\sqrt3}$$

Now, in right $$\triangle$$ EDG, using Pythagoras theorem

=> $$(ED)^2=(EG)^2+(GD)^2$$

=> $$(2r)^2=(s)^2+(s)^2$$

=> $$4r^2=2s^2$$

=> $$s^2=2\times(\frac{a}{2\sqrt3})^2$$

=> $$s^2=\frac{a^2}{6}$$

$$\therefore$$ ar($$\triangle$$) ABC : ar(DEFG)

= $$(\frac{\sqrt3}{4}a^2):(s)^2$$

= $$(\frac{\sqrt3}{4}a^2):(\frac{a^2}{6})$$

= $$3\sqrt3:2$$

=> Ans - (D)