In ΔABC, ∠A : ∠B : ∠C = 3 : 3 : 4. A line parallel to BC is drawn which touches AB and AC at P and Q respectively. What is the value of ∠AQP - ∠APQ?

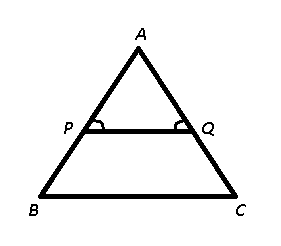
Given : ∠A : ∠B : ∠C = 3 : 3 : 4 and PQ is parallel to BC

To find : ∠AQP - ∠APQ = ?

Solution : Let $$\angle A=3x$$, $$\angle B=3x$$ and $$\angle C=4x$$ 

Thus, in $$\triangle$$ ABC,

=> $$\angle A+\angle B+\angle C=180^\circ$$ 

=> $$3x+3x+4x=180^\circ$$

=> $$x=\frac{180^\circ}{10}=18^\circ$$

$$\because$$ PQ $$\parallel$$ BC, => $$\angle$$ APQ = $$\angle$$ B and $$\angle$$ AQP = $$\angle$$ C  (Corresponding angles)

$$\therefore$$ $$\angle$$ AQP - $$\angle$$ APQ = $$4x-3x=x=18^\circ$$

=> Ans - (B)