A tower standing on a horizontal plane subtends a certain angle at a point 160 m apart from the foot of the tower. On advancing 100 m towards it, the tower is found to subtend an angle twice as before. The height of the tower is

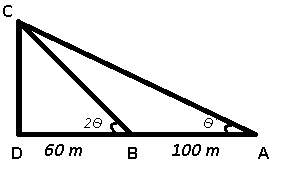
Given : CD is the tower, AD = 160 m and AB = 100 m

=> BD = 160 - 100 = 60 m

To find : CD = $$h$$ = ?

Solution : $$\angle$$ DBC = $$2\theta$$ and $$\angle$$ DAC = $$\theta$$

In $$\triangle$$ ACD,

=> $$tan(\theta)=\frac{CD}{DA}$$

=> $$tan(\theta)=\frac{h}{160}$$ -----------(i)

Similarly, in $$\triangle$$ BCD,

=> $$tan(2\theta)=\frac{CD}{DB}$$

=> $$tan(2\theta)=\frac{h}{60}$$

=> $$\frac{2tan\theta}{1-tan^2\theta}=\frac{h}{60}$$

Substituting value from equation (i), we get :

=> $$2\times\frac{h}{160}=[1-(\frac{h}{160})^2]\times(\frac{h}{60})$$

=> $$\frac{60}{80}=1-(\frac{h}{160})^2$$

=> $$(\frac{h}{160})^2=1-\frac{3}{4}=\frac{1}{4}$$

=> $$\frac{h}{160}=\sqrt{\frac{1}{4}}=\frac{1}{2}$$

=> $$h=\frac{160}{2}=80$$

$$\therefore$$ Height of tower is 80 m

=> Ans - (A)