Question 148

In $$\triangle ABC$$, the external bisectors of the angles $$\angle B$$ and $$\angle C$$ meet at the point O. If $$\angle A=70^\circ$$, then the measure of $$\angle BOC$$ is:

Solution

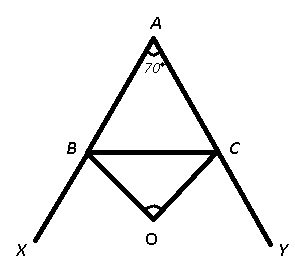
Given : O is excentre of $$\triangle$$ ABC and $$\angle A=70^\circ$$

To find : $$\angle$$ BOC = $$\theta=?$$

Solution : Excentre of a triangle = $$90^\circ-\frac{1}{2} \times $$ (Angle opposite to it)

=> $$\theta=90^\circ-\frac{\angle A}{2}$$

=> $$\theta=90^\circ-\frac{70^\circ}{2}$$

=> $$\theta=90^\circ-35^\circ=55^\circ$$

=> Ans - (D)

Create a FREE account and get: