In $$\triangle$$PQR, S and T are the mid points of sides PQ and PR respectively. If $$\angle$$QPR = $$45^{0}$$ and $$\angle$$PRQ = $$55^{0}$$, then what is the value (in degrees) of $$\angle$$QST ?

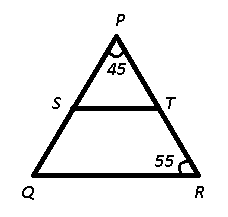
Given : $$\angle$$QPR = $$45^\circ$$ and $$\angle$$PRQ = $$55^\circ$$

To find : $$\angle$$QST = ?

Solution : In triangle, PQR

=> $$\angle P+\angle Q+\angle R=180^\circ$$

=> $$45^\circ+55^\circ+\angle Q=180^\circ$$

=> $$\angle Q=180^\circ-100^\circ=80^\circ$$

Now, since ST divides PQ and PR equally, thus ST is parallel to QR.

$$\therefore$$ Angles on the same side of transversal are supplementary, => $$\angle PQR+\angle QST=180^\circ$$

=> $$\angle QST=180^\circ-80^\circ=100^\circ$$

=> Ans - (D)