In ΔPQR, a line parallel to side QR cuts the side PQ and PR at points M and N respectively and point M divide PQ in the ratio of 1 : 2. If area of ΔPQR is 360 cm2, then what is the area (in cm2) of quadrilateral MNRQ?

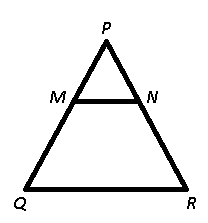
Given = PM : MQ = 1 : 2 and area of $$\triangle$$ PQR = $$360$$ $$cm^2$$

To find = area (MNRQ) = ?

Solution = Since, MN is parallel to QR, => $$\frac{PM}{PQ}=\frac{PN}{PR}=\frac{1}{3}$$

=> $$\triangle PMN \sim \triangle PQR$$

Now, ratio of area of the two triangles is equal to the ratio of square of the corresponding sides.

=> $$\frac{ar(\triangle PMN)}{ar(\triangle PQR)}=(\frac{1}{3})^2$$

=> $$\frac{ar(\triangle PMN)}{360}=\frac{1}{9}$$

=> $$ar(\triangle PMN)=\frac{360}{9}=40$$ $$cm^2$$

$$\therefore$$ $$ar(MNRQ)=360-40=320$$ $$cm^2$$

=> Ans - (B)