Question 131

If the area of the circle in the figure is 36$$\pi$$ sq. cm. And ABCD is a square, then the area of $$\triangle ACD$$, in sq.cm, is

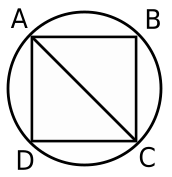
Solution

Area of circle = $$ \pi \times r^2= 36\pi$$ sq.cm

=> $$r = \sqrt{36}=6$$ cm

=> Diameter of circle = $$AC =2r = 12 $$ cm

In $$\triangle$$ ACD, let $$AD=CD=s$$ cm

=> $$(AD)^2+(CD)^2=(AC)^2$$

=> $$2s^2=(12)^2=144$$

=> $$s^2=\frac{144}{2}=72$$ -----------(i)

$$\therefore$$ Area of $$\triangle$$ ACD = $$ \frac{1}{2} \times s \times s$$

= $$\frac{s^2}{2}=36$$ $$cm^2$$

=> Ans - (D)

Create a FREE account and get: