E is the midpoint if the median AD of $$\triangle ABC$$. BE is joined and produced to meet AC at F. F divides AC in the ratio:

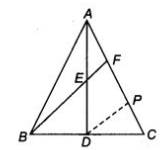
Given : In $$\triangle$$ ABC, AD is the median and E is the mid point of AD.

Construction : Draw DP parallel to EF

To find = AF : FC

Solution : in $$\triangle$$ ADP, E is the mid point of AD and EF$$\parallel$$DP.

=> F is mid point of AP.       [By converse of mid point theorem]

Similarly, in $$\triangle$$ FBC, D is the mid point of BC and EF$$\parallel$$DP.

=> P is mid point of FC.

Thus, AF = FP = PC

$$\therefore$$ $$AF=\frac{1}{3}FC$$

=> F divides AC in the ratio = $$1:3$$

=> Ans - (B)