AC and BC are two equal cords of a circle. BA is produced to any point P and CP, when joined cuts the circle at T. Then

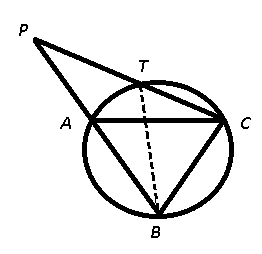
It is given that AC = BC, also $$\triangle$$ PTB and $$\triangle$$ PAC are similar, we have :

$$\frac{CA}{CP}=\frac{BT}{BP}$$ ----------------(i)

Also, we have $$\angle$$ PBC = $$\angle$$ BTC ($$\because$$ $$\angle$$ PBC = $$\angle$$ BAC = $$\angle$$ BTC) and $$\angle$$ PCB = $$\angle$$ BCT

=> $$\triangle$$ PBC $$\sim$$ $$\triangle$$ BTC

Thus, $$\frac{CB}{BP}=\frac{CT}{BT}$$

=> $$\frac{BT}{BP}=\frac{CT}{CB}$$ --------------(ii)

From equations (i) and (ii), we get :

$$\frac{CA}{CP}=\frac{CT}{CB}$$

=> Ans - (C)