Let BE and CF be the two medians of a $$\triangle$$ ABC and G be their intersection. Also let EF cut AG at O. Then AO : OG is

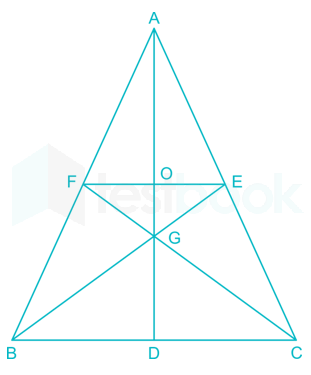
BE and CF are medians and G is their intersection. AD passing through G is also a median. => G is the centroid of $$\triangle$$ ABC

Also, a centroid divides the median in the ratio 2:1, => AG : GD = 2 : 1

Let AD = $$3x$$ units

=> AG = $$2x$$ and GD = $$x$$

Also, E and F are mid points of AC and AB respectively.

We know that line joining mid points of any two sides of a triangle bisects the medians from the vertex which is between the taking sides.

Thus, EF bisects AD

=> AO = OD = $$\frac{3x}{2}$$ units

Now, OG = AG - AO = $$2x-\frac{3x}{2}=\frac{x}{2}$$

$$\therefore$$ AO : OG = $$\frac{3x}{2}:\frac{x}{2}$$

= $$3:1$$

=> Ans - (D)