Question 128
If the external bisector of the vertical angle $$\angle$$ A of the $$\triangle$$ ABC is parallel to the base BC, then the $$\triangle$$ ABC is a/an
Solution
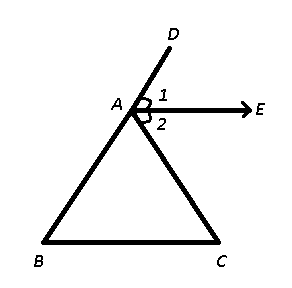
AE is the bisector of the exterior $$\angle$$ DAC of the $$\triangle$$ ABC and AE || BC
Now, $$\angle$$ $$1$$ = $$\angle$$ $$2$$ (given)
Also, $$\angle$$ $$B$$ = $$\angle$$ $$1$$ (Corresponding angle)
and $$\angle$$ $$C$$ = $$\angle$$ $$2$$ (Alternate angle)
=> $$\angle$$ $$B$$ = $$\angle$$ $$C$$
=> AB = AC
So, $$\triangle$$ ABC is an isosceles triangle.
=> Ans - (B)
Get AI Help
Create a FREE account and get:
- Free SSC Study Material - 18000 Questions
- 230+ SSC previous papers with solutions PDF
- 100+ SSC Online Tests for Free
