If the angle of elevation of the sun changes from $$45^0\ to\ 60^0$$, then the length of the shadow of a pillar decreases by 10m. The height of the pillar is:

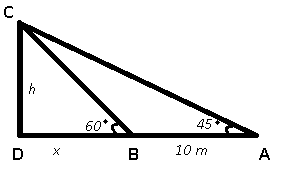
Given : CD is the pillar and AB = 10 m

To find : Height of pillar = $$h$$ = ?

Solution : In $$\triangle$$ ACD,

=> $$tan(45^\circ)=\frac{CD}{AD}$$

=> $$1=\frac{h}{x+10}$$

=> $$h=x+10$$ -------------(i)

Again, in $$\triangle$$ BCD,

=> $$tan(60^\circ)=\frac{CD}{DB}$$

=> $$\sqrt{3}=\frac{h}{x}$$

=> $$h=x\sqrt{3}$$

=> $$h=(h-10)\sqrt3$$     [Using (i)]

=> $$h=h\sqrt3-10\sqrt3$$

=> $$h(\sqrt3-1)=10\sqrt3$$

=> $$h=\frac{10\sqrt3}{\sqrt3-1}$$

Rationalizing the denominator, we get :

=> $$h=\frac{10\sqrt3}{\sqrt3-1}\times\frac{(\sqrt3+1)}{(\sqrt3+1)}$$

=> $$h=\frac{10\sqrt3(\sqrt3+1)}{(3-1)}$$

=> $$h=5\sqrt3(\sqrt3+1)$$

=> $$h=5(3+\sqrt3)$$ m

=> Ans - (D)