The perimetre of a rhombus in 20 cm and one of the diagonal is 8 cm. What is the area (in $$cm^{2}$$) of the rhombus?

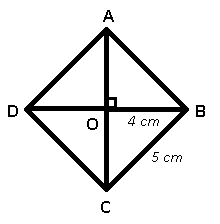
Given : ABCD is the rhombus whose diagonals bisect at O and the diagonals of a rhombus bisect each other at right angle. BD = 8 cm

=> OB = 4 cm

Perimeter of rhombus = 20 cm

=> BC = $$\frac{20}{4}=5$$ cm

Thus, in $$\triangle$$ BOC, 

=> $$(OC)^2=(BC)^2-(OB)^2$$

=> $$(OC)^2 = (5)^2-(4)^2$$

=> $$(OC)^2=25-16=9$$

=> $$OC=\sqrt{9}=3$$ cm

Thus, AC = 6 cm and BD = 8 cm

$$\therefore$$ Area of rhombus = $$\frac{1}{2}\times d_1\times d_2$$

= $$\frac{1}{2}\times6\times8=24$$ $$cm^2$$

=> Ans - (B)