Let ABC be a triangle and AD be the perpendicular from the vertex A on the side BC such that $$AD^{2}$$= BDxCD. Then measure of $$\ \angle\ $$BAC is:

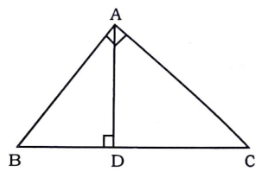
Given : In $$\triangle ABC$$, $$AD \perp BC$$and $$AD^2=BD\times DC$$

To find : $$\angle BAC$$

Solution : In right $$\triangle$$ ADB and $$\triangle$$ ADC, if we apply Pythagoras Theorem,

=> $$(AB)^2=(AD)^2+(BD)^2$$ -------------(i)

and => $$(AC)^2=(AD)^2+(DC)^2$$ -------------(ii)

Adding equations (i) and (ii), we get :

=> $$(AB)^2+(AC)^2=2(AD)^2+(BD)^2+(DC)^2$$

=> $$(AB)^2+(AC)^2=2(BD)(DC)+(BD)^2+(DC)^2$$      [Given]

=> $$(AB)^2+(AC)^2=(BD+DC)^2$$

=> $$(AB)^2+(AC)^2=(BC)^2$$

Hence, $$\triangle$$ ABC is a right triangle right angled at A.

$$\therefore$$ $$\angle$$ BAC = $$90^\circ$$

=> Ans - (A)