Question 123
ABCD is a square. Draw a triangle QBC on side BC considering BC as base and draw a triangle PAC on AC as its base such that $$\triangle QBC\sim\triangle PAC$$, Then $$\frac{Area\ of\ \triangle QBC}{Area\ of\ \triangle PAC}$$ is equal to:
Solution
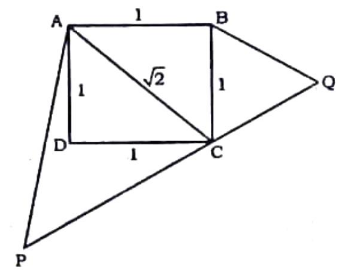
Let side of square ABCD = 1 unit
=> Diagonal AC = $$\sqrt{1^2+1^2}=\sqrt2$$ units
It is given that $$\triangle QBC\sim\triangle PAC$$
Ratio of areas of two similar triangles is equal to the ratio of squares of corresponding sides.
=>Â $$\frac{Area\ of\ \triangle QBC}{Area\ of\ \triangle PAC}=\frac{(BC)^2}{(AC)^2}$$
= $$\frac{1^2}{(\sqrt2)^2}$$
= $$\frac{1}{2}$$
=> Ans - (C)
Create a FREE account and get:
- Free SSC Study Material - 18000 Questions
- 230+ SSC previous papers with solutions PDF
- 100+ SSC Online Tests for Free
