Two concentric circles are drawn with radii 12 cm and 13 cm. What will be the length of any chord of the larger circle that is tangent to the smaller circle ?

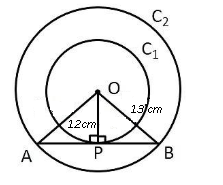
Given : $$C_1$$ and $$C_2$$ be the two concentric circles having radius $$r_1=13$$ cm and $$r_2=12$$ cm respectively.

To find : AB = ?

Solution : AB is the the tangent to the circle $$C_1$$, hence $$\angle$$ OPB = $$90^\circ$$

Also, the perpendicular from the centre of a circle to a chord bisects the chord.

Thus, in $$\triangle$$ OPB,

=> $$(PB)^2=(OB)^2-(OP)^2$$

=> $$(PB)^2=(13)^2-(12)^2$$

=> $$(PB)^2=169-144=25$$

=> $$PB=\sqrt{25}=5$$ cm

$$\therefore$$ AB = $$2\times5=10$$ cm

=> Ans - (C)