A vertical pole AB is standing at the centre B of a square PQRS. If PR subtends an angle of $$90^{0}$$at the top A of the pole, then the angle subtended by a side of the square at A is:

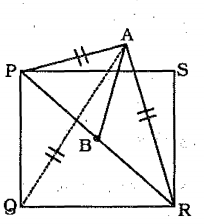
The pole is standing at the centre of the square, => PA = PR

=> $$\angle$$ APB = $$\angle$$ ARB = $$45^\circ$$

Let the side of the square = $$x$$ units

=> PR (diagonal) = $$\sqrt2x$$ units

Hence, PB = $$\frac{x}{\sqrt2}$$ units

Now, in $$\triangle$$ APB,

=> $$tan(\angle APB)=\frac{AB}{PB}$$

=> $$tan(45^\circ)=1=\frac{AB}{PB}$$

=> $$AB=PB=\frac{x}{\sqrt2}$$

Thus, $$PA=\sqrt{(\frac{x}{\sqrt2})^2+(\frac{x}{\sqrt2})^2}$$

=> $$PA=\sqrt{\frac{x^2}{2}+\frac{x^2}{2}}=\sqrt{x^2}=x$$

Similarly, $$QA=x$$ units

Hence, PA = PQ = QA = $$x$$

$$\therefore$$ $$\angle$$ PAQ = $$60^\circ$$

=> Ans - (C)