In $$\triangle ABC, \angle B=60^\circ$$, and $$\angle C=40^\circ$$, AD and AE are respectively the bisector of $$\angle A$$ and perpendicular on BC. The measure of $$\angle EAD$$ is:

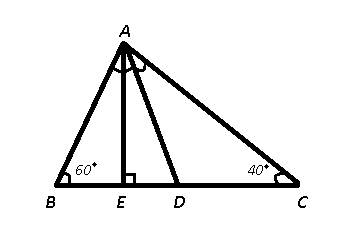
Given : AD is angle bisector of $$\angle$$ A and AE is perpendicular to BC.

To find : $$\angle$$ EAD = ?

In $$\triangle$$ ABC,

=> $$\angle$$ A + $$\angle$$ B + $$\angle$$ C = $$180^\circ$$

=> $$\angle$$ A + $$60^\circ+40^\circ=180^\circ$$

=> $$\angle$$ A = $$180^\circ-100^\circ=80^\circ$$

$$\because$$ $$\angle$$ BAD = $$\angle$$ CAD

=> $$\angle$$ CAD = $$\frac{80}{2}=40^\circ$$

Using external angle property, => $$\angle$$ ADE = $$\angle$$ CAD + $$\angle$$ C

=> $$\angle$$ ADE = $$40^\circ+40^\circ=80^\circ$$

$$\therefore$$ In $$\triangle$$ EAD,

=> $$\angle$$ EAD + $$\angle$$ ADE + $$\angle$$ DEA = $$180^\circ$$

=> $$\angle$$ EAD + $$80^\circ+90^\circ=180^\circ$$

=> $$\angle$$ EAD = $$180^\circ-170^\circ=10^\circ$$

=> Ans - (D)