150 workers were engaged to finish a piece of work in a certain number of days. Four workers dropped on the second day, four more workers dropped on third day and so on. It takes 8 more days to finish the work no. Find the number of days in which the work was completed ?
Solution
Let 1 worker does 1 unit work in a day.
Let 150 workers can finish the work in $$(n-8)$$ days, if all workers work all the days.
Then, total work
Also, 150 workers work on day 1, 146 workers work on day 2, ... and so on. Work is completed in $$n$$ days.
Thus, total work = $$150+146+....(n$$ terms$$)$$
This is an arithmetic progression with first term, $$a=150$$, $$d=-4$$.
Thus, total work = $$\frac{n}{2}[2a+(n-1)d]$$
= $$\frac{n}{2}[2(150)+(n-1)(-4)]$$
= $$\frac{n}{2}[300-4n+4]$$
= $$\frac{n}{2}[304-4n]=n(152-2n)$$ -------------(ii)
Comparing equations (i) and (ii),
=> $$150(n-8)=n(152-2n)$$
=> $$75(n-8)=n(76-n)$$
=> $$75n-600=76n-n^2$$
=> $$n^2-n-600=0$$
=> $$(n-25)(n+24)=0$$
=> $$n=25,-24$$
$$\because n$$ cannot be negative, => $$n=25$$
=> Number of days in which the work was completed = 25
=> Ans - (D)
Video Solution
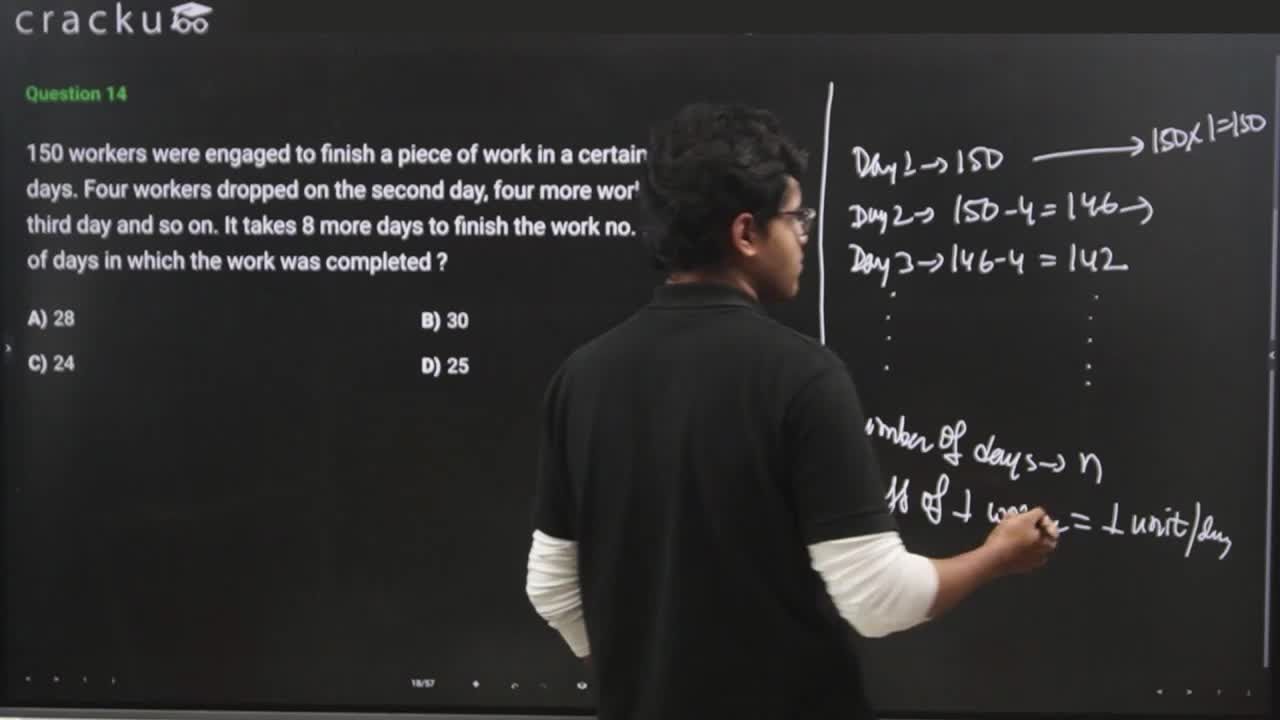
Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
- Free SSC Study Material - 18000 Questions
- 230+ SSC previous papers with solutions PDF
- 100+ SSC Online Tests for Free

