A right circular cone is enveloping a right circular cylinder such that the base of the cylinder rests on the base of the cone. If the radius and the height of the cone is 4 cm and 10 cm respectively, then the largest possible curved surface area of the cylinder of radius r is:

Top face will look like the figure shown below. 

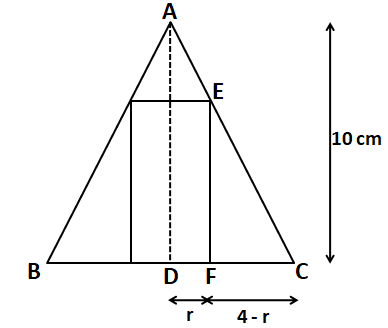
Curved surface area of the cylinder = $$2*\pi*r*h$$

To calculate height of the cylinder in terms of 'r', we can see that $$\triangle$$ADC is similar to $$\triangle$$EFC. 

Therefore, 

$$\dfrac{AD}{DC}=\dfrac{EF}{FC}$$

$$\Rightarrow$$ $$\dfrac{10}{4} = \dfrac{h}{4-r}$$

$$\Rightarrow$$ $$h = \dfrac{5}{2}(4-r)$$

Therefore, the curved surface area of the cylinder = $$2*\pi*r*\dfrac{5}{2}(4-r)$$ = $$5πr(4 - r)$$.

Hence, option B is the correct answer.