Instructions

Study the following table and answer the question:
Number of students enrolled for Vocational Courses (VC) in five institutes - A, B, C, D & E.

Question 65

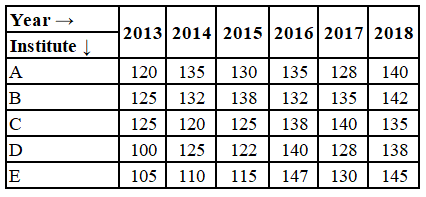
What is the sum of the average number of students enrolled for VC in institute B in 2014, 2015 and 2017 and the average number of students enrolled in institute E in 2013 and 2018?

Solution

Average number of students enrolled for VC in institute B in 2014, 2015 and 2017 = $$\frac{132+138+135}{3}$$

= $$\frac{405}{3}$$

= 135

Average number of students enrolled in institute E in 2013 and 2018 = $$\frac{105+145}{2}$$

= $$\frac{250}{2}$$

= 125

Required sum = 135 + 125

= 260

Hence, the correct answer is Option C

Create a FREE account and get: