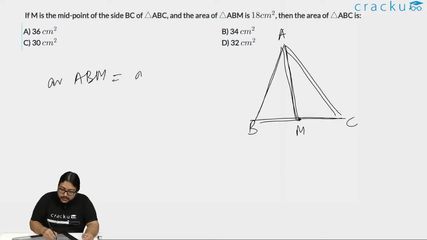
If M is the mid-point of the side BC of $$\triangle$$ABC, and the area of $$\triangle$$ABM is $$18 cm^2$$, then the area of $$\triangle$$ABC is:

Let AD is the perpendicular to BC

Given,

Area of the $$\triangle$$ABM = $$18 cm^2$$

$$=$$>  $$\frac{1}{2}\times \text{AD}\times \text{BM}$$ = $$18 cm^2$$

M is the mid-point of BC

$$=$$>  BM = MC

Area of the $$\triangle$$ACM = $$\frac{1}{2}\times \text{AD}\times \text{MC}=\frac{1}{2}\times \text{AD}\times \text{BM}=18cm^2$$

$$\therefore\ $$Area of the $$\triangle$$ABC = Area of the $$\triangle$$ABM + Area of the $$\triangle$$ACM = $$18+18=36cm^2$$

Hence, the correct answer is Option A