The centroid of an equilateral $$\triangle$$XYZ is L. If XY = 12 cm, then the length of XL (in cm), is:

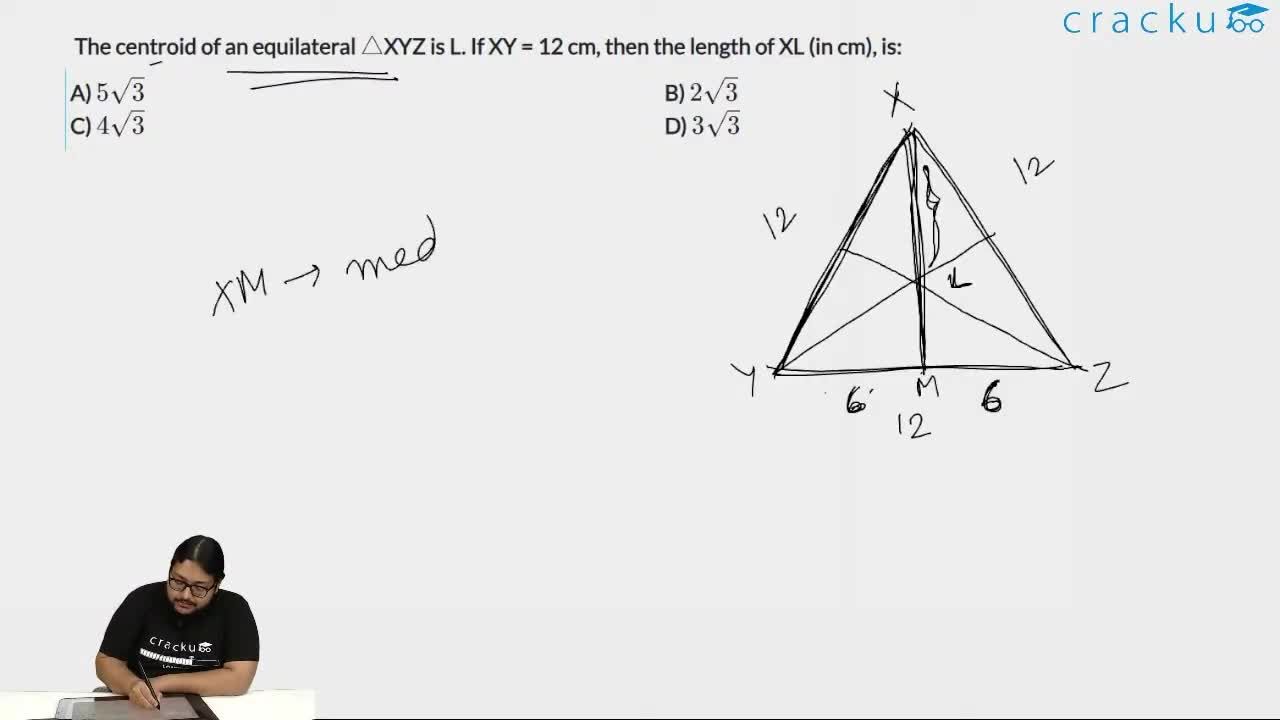
In the equilateral traingle XYZ,  XY = 12 cm

$$\Rightarrow$$  YZ = XZ = 12 cm

The median XP bisects YZ at P and also perpendicular to YZ in the equilateral triangle.

$$\Rightarrow$$  YP = PZ = 6 cm   and  XP$$\bot\ $$YZ

The centroid L divides the median XP in the ratio of 2 : 1

$$\Rightarrow$$ XL : PL = 2 : 1

$$\Rightarrow$$ XL = 2PL .............(1)

In $$\triangle$$XPZ,

XP$$^2$$ + PZ$$^2$$ = XZ$$^2$$

$$\Rightarrow$$ XP$$^2$$ + 6$$^2$$ = 12$$^2$$

$$\Rightarrow$$ XP$$^2$$ + 36 = 144

$$\Rightarrow$$  XP$$^2$$ = 108

$$\Rightarrow$$  XP = $$6\sqrt{3}$$

$$\Rightarrow$$  XL + PL = $$6\sqrt{3}$$

$$\Rightarrow$$  2PL + PL = $$6\sqrt{3}$$

$$\Rightarrow$$  3PL = $$6\sqrt{3}$$

$$\Rightarrow$$  PL = $$2\sqrt{3}$$

$$\Rightarrow$$  XL = 2PL = $$4\sqrt{3}$$

Hence, the correct answer is Option C